以下文章来源于公众号【程序员小灰】 ,作者小灰 本文仅作为个人数据结构复习,如有侵权,请联系本文作者删除~
😀 给定一个有序数组,如何根据元素的值进行高效率查找?
🍒 二分查找:首先根据数组下标,定位到数组的中间元素,判断要查找的元素是否大于中间元素,若大于,再次定位到数组右半部分的中间元素,否则则定位到左半部分的中间元素,以此类推。
如果数组的长度是n,二分查找的时间复杂度是O(logn),比起从左到右逐个遍历元素进行查找的方式,大大提升了查找性能。
😀 若给定的是有序链表呢?
🍒 传统只能从头节点开始顺着next指针逐个访问下一个节点,没法做二分查找。
但可以做一个升级 👇 (就像翻书一样,对应的部、章、节等)
索引链表
增加索引链表
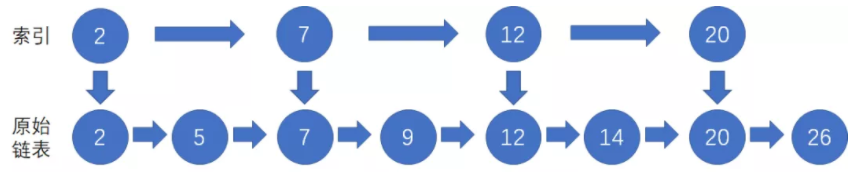
增加索引链表,当我们想要定位到结点20,我们不需要在原始链表中一个一个结点访问,而是首先访问索引链表,在索引链表找到结点20之后,我们顺着索引链表的结点向下,找到原始链表的结点20。
由于索引链表的结点个数是原始链表的一半,查找结点所需的访问次数也相应减少了一半。当链表的索引分成更多的层次时,查找效率也会更快。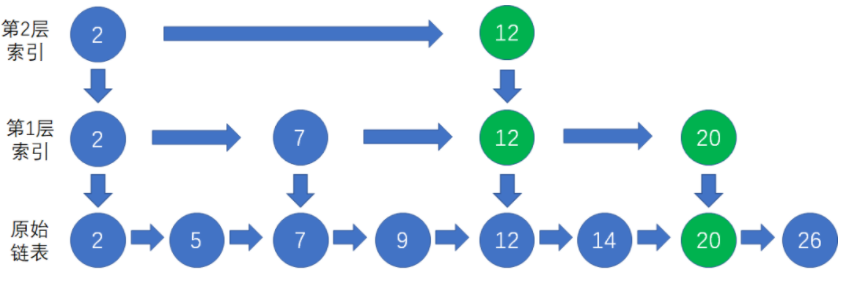
抽出了第二层更为稀疏的索引,节点数量是第一层索引的一半,从最上层的索引开始查找。
当节点数量更多时,可以抽出更多的索引层级,每一层索引的节点数量都是底层索引的一半。
时空效率(以空间换时间)
假设原始链表有n个结点,那么索引的层级就是 $log(n)-1$,在每一层的访问次数是常量,因此查找结点的平均时间复杂度是$O(logn)$。这比起常规的查找方式,也就是线性依次访问链表节点的方式,效率要高得多。
但相应的,这种基于链表的优化增加了额外的空间开销。假设原始链表有n个结点,那么各层索引的结点总数是$n/2+n/4+n/8+n/16+……2≈n$。
也就是说,优化之后的数据结构所占空间,是原来的2倍。这是典型的以空间换时间的做法。
跳表(SkipList)
向上面这样基于链表改造的数据结构叫做跳表
插入操作
假设我们要插入的结点是10,首先我们按照跳表查找结点的方法,找到待插入结点的前置结点(仅小于待插入结点)。然后按照一般链表的插入方式,把结点10插入到结点9的下一个位置。
插入操作不止如此。
随着原始链表的新结点越来越多,索引会渐渐变得不够用了,因此索引结点也需要相应作出调整。
如何调整索引呢?我们让新插入的结点随机“晋升”,也就是成为索引结点。新结点晋升成功的几率是50%。
假设第一次随机的结果是晋升成功,那么我们把结点10作为索引结点,插入到第1层索引的对应位置,并且向下指向原始链表的结点10:
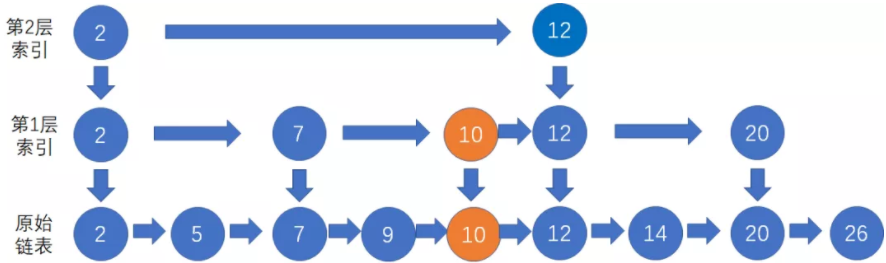
新结点在成功晋升之后,仍然有机会继续向上一层索引晋升。我们再进行一次随机,假设随机的结果是晋升失败,那么插入操作就告一段落了。
当新节点晋升到第二层索引,下一次随机的结果仍然是晋升成功,就直接让索引增加一层
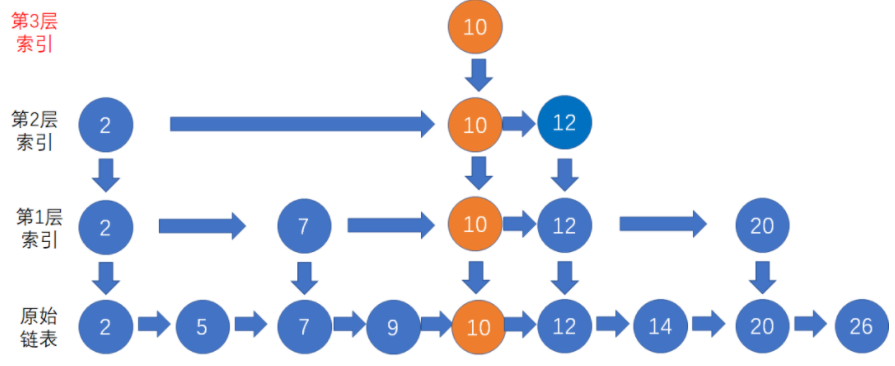
删除操作(相反思路)
先找到要删除的节点,把节点从原始链表中删除,并且把索引中对应的节点也删除掉。
如果某一层索引节点被删光了,直接把失去节点的那一层删掉。
代码实现
上面画的跳表是经过简化后的,和实际代码实现有些出入,具体差别如下:
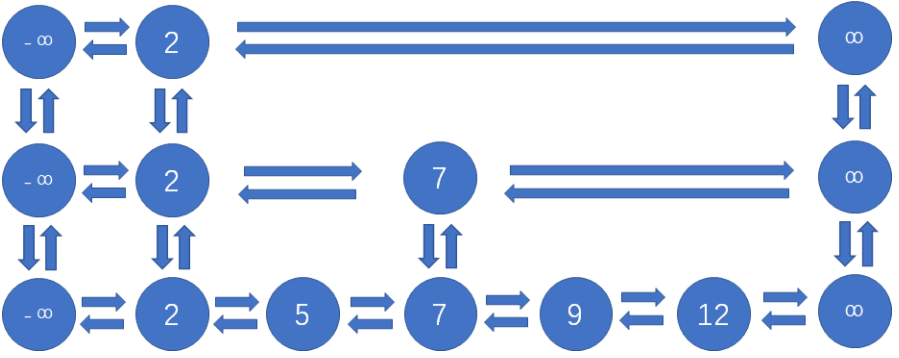
- 程序中跳表采用的是双向链表,无论前后结点还是上下结点,都各有两个指针相互指向彼此。
- 程序中跳表的每一层首位各有一个空结点,左侧的空节点是负无穷大,右侧的空节点是正无穷大。
public class SkipList{
//结点“晋升”的概率
private static final double PROMOTE_RATE = 0.5;
private Node head,tail;
private int maxLevel;
public SkipList() {
head = new Node(Integer.MIN_VALUE);
tail = new Node(Integer.MAX_VALUE);
head.right = tail;
tail.left = head;
}
//查找结点
public Node search(int data){
Node p= findNode(data);
if(p.data == data){
System.out.println("找到结点:" + data);
return p;
}
System.out.println("未找到结点:" + data);
return null;
}
//找到值对应的前置结点
private Node findNode(int data){
Node node = head;
while(true){
while (node.right.data!=Integer.MAX_VALUE && node.right.data<=data) {
node = node.right;
}
if (node.down == null) {
break;
}
node = node.down;
}
return node;
}
//插入结点
public void insert(int data){
Node preNode= findNode(data);
//如果data相同,直接返回
if (preNode.data == data) {
return;
}
Node node=new Node(data);
appendNode(preNode, node);
int currentLevel=0;
//随机决定结点是否“晋升”
Random random = new Random();
while (random.nextDouble() < PROMOTE_RATE) {
//如果当前层已经是最高层,需要增加一层
if (currentLevel == maxLevel) {
addLevel();
}
//找到上一层的前置节点
while (preNode.up==null) {
preNode=preNode.left;
}
preNode=preNode.up;
//把“晋升”的新结点插入到上一层
Node upperNode = new Node(data);
appendNode(preNode, upperNode);
upperNode.down = node;
node.up = upperNode;
node = upperNode;
currentLevel++;
}
}
//在前置结点后面添加新结点
private void appendNode(Node preNode, Node newNode){
newNode.left=preNode;
newNode.right=preNode.right;
preNode.right.left=newNode;
preNode.right=newNode;
}
//增加一层
private void addLevel(){
maxLevel++;
Node p1=new Node(Integer.MIN_VALUE);
Node p2=new Node(Integer.MAX_VALUE);
p1.right=p2;
p2.left=p1;
p1.down=head;
head.up=p1;
p2.down=tail;
tail.up=p2;
head=p1;
tail=p2;
}
//删除结点
public boolean remove(int data){
Node removedNode = search(data);
if(removedNode == null){
return false;
}
int currentLevel=0;
while (removedNode != null){
removedNode.right.left = removedNode.left;
removedNode.left.right = removedNode.right;
//如果不是最底层,且只有无穷小和无穷大结点,删除该层
if(currentLevel != 0 && removedNode.left.data == Integer.MIN_VALUE && removedNode.right.data == Integer.MAX_VALUE){
removeLevel(removedNode.left);
}else {
currentLevel ++;
}
removedNode = removedNode.up;
}
return true;
}
//删除一层
private void removeLevel(Node leftNode){
Node rightNode = leftNode.right;
//如果删除层是最高层
if(leftNode.up == null){
leftNode.down.up = null;
rightNode.down.up = null;
}else {
leftNode.up.down = leftNode.down;
leftNode.down.up = leftNode.up;
rightNode.up.down = rightNode.down;
rightNode.down.up = rightNode.up;
}
maxLevel --;
}
//输出底层链表
public void printList() {
Node node=head;
while (node.down != null) {
node = node.down;
}
while (node.right.data != Integer.MAX_VALUE) {
System.out.print(node.right.data + " ");
node = node.right;
}
System.out.println();
}
//链表结点类
public class Node {
public int data;
//跳表结点的前后和上下都有指针
public Node up, down, left, right;
public Node(int data) {
this.data = data;
}
}
public static void main(String[] args) {
SkipList list=new SkipList();
list.insert(50);
list.insert(15);
list.insert(13);
list.insert(20);
list.insert(100);
list.insert(75);
list.insert(99);
list.insert(76);
list.insert(83);
list.insert(65);
list.printList();
list.search(50);
list.remove(50);
list.search(50);
}
}
总结
跳表是基于链表的升级,使得有序链表获得高校增删改查,并始终维持有序的能力。
功能和性能上与红黑树相似,但是是线上远比红黑树简单。