LeetCode 二叉树

DFS & BFS总结

刷题过程的一些总结~

Posted by CY on August 16, 2020

网格结构中的DFS

摘自：公众号【面向大象编程】

网格问题基本概念/性质

image-20200816115649515

DFS遍历方法与技巧

二叉树DFS基本结构
void traverse(TreeNode root) {
    // 判断 base case
    if (root == null) {
        return;
    }
    // 访问两个相邻结点：左子结点、右子结点
    traverse(root.left);
    traverse(root.right);
}
网格结构
  • base case：网格中不需要继续遍历的，网格边缘（叶节点）超出网格范围的（相当于root==null）
  • 对于格子 (r, c) 来说（r 和 c 分别代表行坐标和列坐标），四个相邻的格子分别是 (r-1, c)、(r+1, c)、(r, c-1)、(r, c+1)
  • 为了避免重复遍历——标记已经遍历过的格子
网格 DFS 遍历的框架代码
void dfs(int[][] grid, int r, int c) {
    // 判断 base case
    // 如果坐标 (r, c) 超出了网格范围，直接返回
    if (!inArea(grid, r, c)) {
        return;
    }
    // 如果已经遍历过，直接返回
    if (grid[r][c] != 1) {
        return;
    }
    grid[r][c] = 2; // 将格子标记为「已遍历过」
    // 访问上、下、左、右四个相邻结点
    dfs(grid, r - 1, c);
    dfs(grid, r + 1, c);
    dfs(grid, r, c - 1);
    dfs(grid, r, c + 1);
}

// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {
    return 0 <= r && r < grid.length 
         && 0 <= c && c < grid[0].length;
}

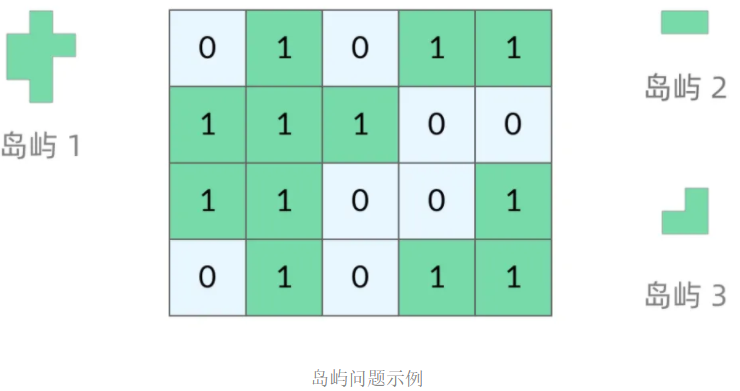
岛屿问题的解法

岛屿的最大面积_leetcode695

给定一个包含了一些 0 和 1 的非空二维数组 grid，一个岛屿是一组相邻的 1（代表陆地），这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0（代表海洋）包围着。

找到给定的二维数组中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

public int maxAreaOfIsland(int[][] grid){
    int ans=0;
    for(int r=0; r< grid.length(); r++){
        for(int c=0; c<grid[0].length(); c++){
            if(grid[r][c]==1){
                int a = dfs(grid, r, c);
                ans=Math.max(ans,a);
            }
        }
    }
    return ans;
}

int dfs(int[][] grid, int r, int c){
    if(!inArea(grid,r,c)) return 0;
    if(grid[r][c]!=1) return 0;
    grid[r][c]=2;
    
    return 1+dfs(grid, r-1,c)
        +dfs(grid,r+1,c)
        +dfs(grid,r,c-1)
        +dfs(grif,r,c+1);
}

boolean inArea(int[][] grid, int r, int c){
    return r>=0 && r<grid.length()
        && c>=0 && c>grid[0].length();
}
填海造陆问题_leetcode827

在二维地图上， 0 代表海洋，1代表陆地，我们最多只能将一格 0 （海洋）变成 1 （陆地）。进行填海之后，地图上最大的岛屿面积是多少？

岛屿的周长_leetcode463

实际上，岛屿的周长是计算岛屿全部的「边缘」，而这些边缘就是我们在 DFS 遍历中，dfs 函数返回的位置。观察题目示例，我们可以将岛屿的周长中的边分为两类，如下图所示。黄色的边是与网格边界相邻的周长，而蓝色的边是与海洋格子相邻的周长。

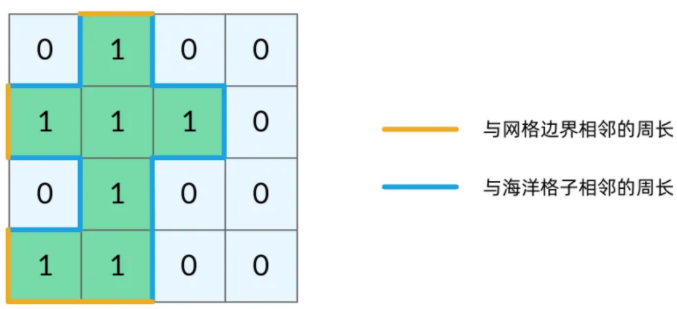
image-20200816125408805

当 dfs 函数因为「坐标 (r, c) 超出网格范围」返回的时候，实际上就经过了一条黄色的边；而当函数因为「当前格子是海洋格子」返回的时候，实际上就经过了一条蓝色的边。

BFS 的使用场景总结：层序遍历、最短路径问题

摘自：leetcode

DFS 与 BFS 的特点比较

// DFS遍历使用递归：
void dfs(TreeNode root){
    if (root==null) return;
    dfs(root.left);
    dfs(root.right);
}

//BFS遍历使用队列：
void bfs(TreeNode root){
    Queue<TreeNode> queue = new ArrayDeque<>();
    queue.add(root); //队列尾部插入root
    while(!queue.isEmpty()){
        //取出队列头部元素，并从队列中移除； 队列为空，返回null
        TreeNode cur = queue.poll(); 
        if(cur.left!=null)  queue.add(cur.left);
        if(cur.right!=null) queue.add(cur.right);  
    }
}

Deque接口集成自Queue，支持同时从两端添加。ArrayDeque是Deque接口的一种具体实现， 底部是使用数组存储元素，同时还使用了两个索引来表征当前数组的状态，分别是 head 和 tail。head 是头部元素的索引，但注意 tail 不是尾部元素的索引，而是尾部元素的下一位，即下一个将要被加入的元素的索引。

ArrayDeque 没有容量限制，可根据需求自动进行扩容。ArrayDeque 可以作为栈来使用，效率要高于 Stack；ArrayDeque 也可以作为队列来使用，效率相较于基于双向链表的 LinkedList 也要更好一些。ArrayDeque 不支持为 null 的元素。

参考资料

BFS 的适用场景

层序遍历、最短路径

如何用 BFS 进行层序遍历_leetcode102

层序遍历要求输出每一层，返回二维数组，但BFS遍历结果是一个一维数组，无法区分每一层

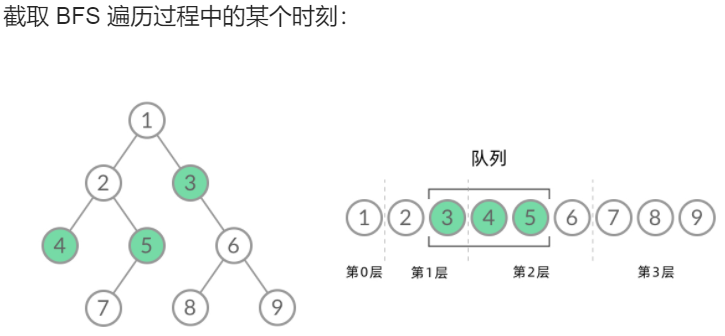
image-20200815181939824

此时队列中的节点分别来自不同层，无法区分队列中的节点来自哪一层

因此稍微修改一下代码——在每一层遍历开始之前，先记录队列中的节点数量n（即这一层的节点数量），然后一次性处理完这一层的n个节点

void dfs(TreeNode root){
    Queue<TreeNode> queue = ArrayDeque<>();
    queue.add(root);
    //在while循环的每一轮，都是将当前层的所有节点出队列，再将下一层的所有节点入队列
    while(!queue.isEmpty()){
        int n = queue.size();
        for(int i=0; i<n; i++){
            TreeNode cur = queue.poll();
            if(cur.left!=null) queue.add(cur.left);
            if(cur.right!=null) queue.add(cur.right);
        }

    }
}

因此层序遍历的完整实现：

public List<List<Integer>> levelOrder(TreeNode root) {
    List<List<Integer>> ans = new ArrayList<>();
    Queue<TreeNode> queue = new ArrayDeque<>();
    if(root!=null) queue.add(root);
    while(!queue.empty()){
        int n = queue.size();
        List<Integer> level = new ArrayList<>();
        for(int i=0; i<n; i++){
            TreeNode cur=queue.poll();
            level.add(node.val);
            if(cur.left) queue.add(cur.left);
            if(cur.right) queue.add(cur.right);
        }
        ans.add(level);
    }

如何用 BFS 求解最短路径问题_leetcode 1162

Dijkstra算法也是解决最短路径——带权最短路径。这里关注的是无权最短路，可以看成每边权重为1，这样的问题用BFS求解即可。

题目

你现在手里有一份大小为 $n \times n$ 的地图网格 grid，上面的每个单元格都标记为 0 或者 1，其中 0 代表海洋，1 代表陆地，请你找出一个海洋区域，这个海洋区域到离它最近的陆地区域的距离是最大的。

我们这里说的距离是「曼哈顿距离」。$(x_0, y_0)$和$(x_1, y_1)$这两个区域之间的距离是 \(\vert x_0 - x_1\vert + \vert y_0 - y_1\vert\)。如果我们的地图上只有陆地或者海洋，请返回 -1。

网格BFS
void bfs(int[][] gird, int r, int c){
    Queue<int[]> queue = new Queue<>();
    //队列存放格子的纵坐标和横坐标
    queue.add(int[]{r,c});
    while(!queue.isEmpty()){
        int n = queue.size();
        for(int i=0; i<n; i++){
            int[] cur = queue.poll();
            int r = cur[0];
            int c = cur[1];
            if(r-1>=0 && grid[r-1][c]==0){
                grid[r-1][c]=2;
                queue.add(new int[]{r-1,c});
            }
            if(r+1<N && grid[r+1][c]==0){
                grid[r+1][c]=2;
                queue.add(new int[]{r+1,c});
            }
            if(c-1>=0 && grid[r][c-1]==0){
                grid[r][c-1]=2;
                queue.add(new int[]{r,c-1});
            }
            if(c+1<N && grid[r][c+1]==0){
                grid[r][c+1]=2;
                queue.add(new int[]{r,c+1});
            }
        }
    }
}

优化：上面代码判断了四次坐标的合法性，有点啰嗦，可以用move数组存储相邻格子的四个方向


int[][] move={{-1,0},{1,0},{0,-1},{0,1}}


void dfs(int[][] grid, int r, int c){
    Queue<int[]> queue = new Queue<>();
    queue.add(new int[]{r,c});
    
    while(!queue.isEmpty()){
        int n = queue.size();
        for(int i=0; i<n; i++){
            int[] cur = queue.poll();
        	r = cur[0];	  c=cur[1];
        	for(int j=0; j<4; j++){
                int rr = r+move[j][0];
                int cc = r+move[j][1];
                if(inArea(grid, rr, cc) && grid[rr][cc]==0){
                    grid[rr][cc]=2;
                    queue.add(new int[]{rr,cc});
                }
            }
        }
    }
}

这题要找的是距离陆地最远的海洋格子，假设网格中只有一个陆地格子，就可以从这个陆地格子出发做层序遍历，直到所有格子都遍历完，最终遍历了几层，海洋格子的最远距离就是几。

当有多个陆地格子的时候，BFS可以以多个多个格子同时作为起点，将所有陆地格子同时放入队列中，然后开始层序遍历——「多源 BFS」

public int maxDistance(int[][] grid) {
    int N = grid.length;

    Queue<int[]> queue = new ArrayDeque<>();
    // 将所有的陆地格子加入队列
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            if (grid[i][j] == 1) {
                queue.add(new int[]{i, j});
            }
        }
    }

    // 如果地图上只有陆地或者海洋，返回 -1
    if (queue.isEmpty() || queue.size() == N * N) {
        return -1;
    }

    int[][] moves = {
        {-1, 0}, {1, 0}, {0, -1}, {0, 1},
    };
    
    //distance记录当前遍历的层数（距离）,不需要给每个遍历到的格子标记层数
    int distance = -1; 
    while (!queue.isEmpty()) {
        distance++;
        int n = queue.size();
        for (int i = 0; i < n; i++) { 
            int[] node = queue.poll();
            int r = node[0];
            int c = node[1];
            for (int[] move : moves) {
                int r2 = r + move[0];
                int c2 = c + move[1];
                if (inArea(grid, r2, c2) && grid[r2][c2] == 0) {
                    grid[r2][c2] = 2;
                    queue.add(new int[]{r2, c2});
                }
            }
        }
    }

    return distance;
}

// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {
    return 0 <= r && r < grid.length 
        && 0 <= c && c < grid[0].length;
}

作者：nettee
链接：https://leetcode-cn.com/problems/binary-tree-level-order-traversal/solution/bfs-de-shi-yong-chang-jing-zong-jie-ceng-xu-bian-l/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
CATALOG
    FEATURED TAGS
    Git 终端 Deep Learning Blog Federated Learning LeetCode 搜索引擎 Reinforcement Learning